5645. Lucky Interval
time limit per test
4 secondsmemory limit per test
512 megabytesinput
standard inputoutput
standard outputPetya loves lucky numbers. We all know that lucky numbers are the positive integers whose decimal representations contain only the lucky digits 4 and 7. For example, numbers 47, 744, 4 are lucky and 5, 17, 467 are not.
One day Petya came across an interval of numbers [a,a+l-1]. Let F(x) be the number of lucky digits of number x. Find the minimum b (a<b) such, that F(a) = F(b), F(a+1) = F(b+1), ..., F(a+l-1) = F(b+l-1).
Input
The single line contains two integers a and l (1≤a,l≤109) − the interval's first number and the interval's length correspondingly.
Output
On the single line print number b − the answer to the problem.
Examples
Input
7 4
Output
17
Input
4 7
Output
14
Note
Consider that [a,b] denotes an interval of integers; this interval includes the boundaries. That is,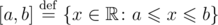 
| 难度等级： | 4 |
| 总通过次数： | 0 |
| 总提交次数： | 0 |
- 进程